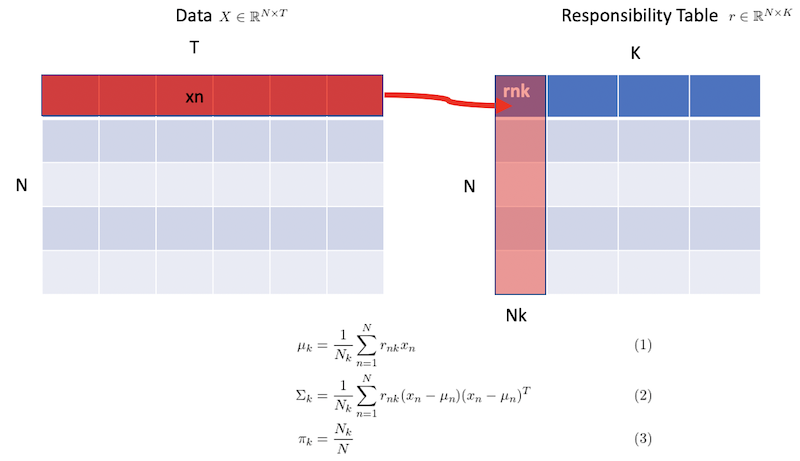
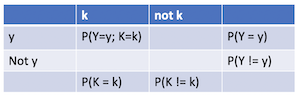
This is the equation
(1) 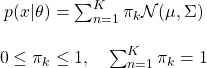
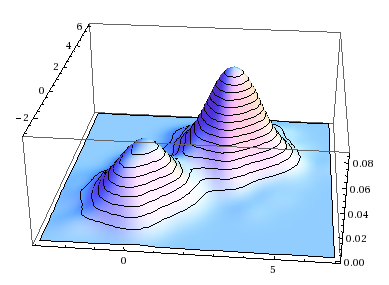
This is the parameters we are going to learn
(2) ![]()
Algorithm
Step 1: Initialization
![]() = mean generated from K-means or randomly selected data point.
= mean generated from K-means or randomly selected data point.
![]() , the equal probability
, the equal probability
![]() = covariance of this dataset
= covariance of this dataset
Step 2: E-Step (get responsibility)
(3) 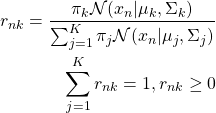
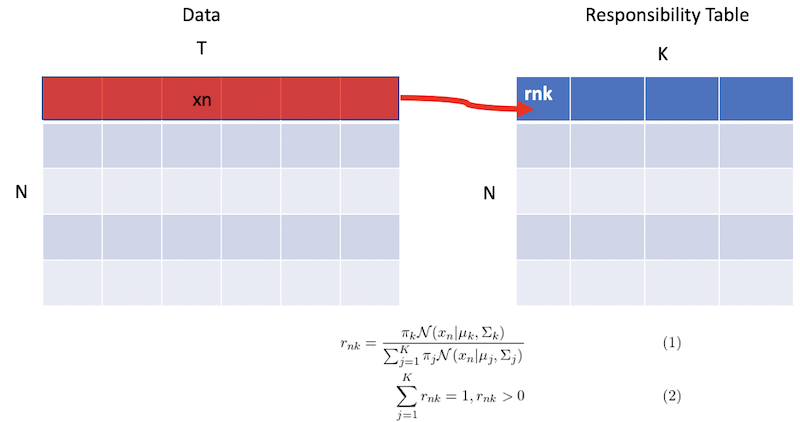
Step 3: M-Step (update ![]() ,
, ![]() ,
, ![]() )
)
(4) 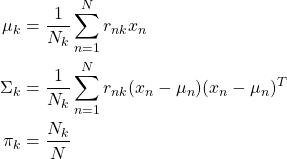
Where ![]() is the weighted mean,
is the weighted mean, ![]() is the weighted variance,
is the weighted variance, ![]() is the normalized probability.
is the normalized probability.