The probability density function (PDF) for the Gaussian Distribution is as follows:
(1) ![]()
Where ![]() is the mean or expection of the distribution (same as median and model).
is the mean or expection of the distribution (same as median and model). ![]() is the standard deviation and
is the standard deviation and ![]() is the variance.
is the variance.
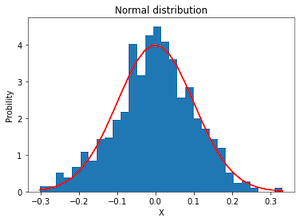
mu, sigma = 0, 0.1 # mean and standard deviation
x = np.random.normal(mu, sigma, 1000)
count, bins, ignored = plt.hist(x, 30, density=True)
y = 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (bins - mu)**2 / (2 * sigma**2) )
plt.plot(bins, y, linewidth=2, color='r')
plt.xlabel('X')
plt.ylabel('Probility')
plt.title('Normal distribution')
plt.show()It is often written as
(2) ![]()
Calculate mean, expectation, median, mode.
Calculate standard deviation, variance, covariance.